[선물거래와 스왑가치평가] 선물 기초, 선물 균형방정식, 선물가격과 기대현물가격, 선물거래전략, 주가지수선물, 금리선물, 스왑
by 펭협
1. 선물의 기초
(1) 선물거래와 현물거래
| 구분 | 현재시점 | 만기시점 |
| 현물거래 | 매매계약 체결 & 대금결제 상품의 인수도 |
|
| 선물거래 | 매매계약 체결 | 대금결제 상품의 인수도 |
🖍 만기일에는 선물가격($F_T$)과 현물가격($S_T$)가 같아짐(베이시스 수렴의 법칙)
(2) 선물거래의 구성
기초자산, 만기일, 선물가격(만기일에 기초자산을 사고 팔 때 적용되는 가격)
(3) 선물거래와 선도가격
| 구분 | 선물거래 | 선도거래 |
| 거래장소 | 공인된 거래소 | 장외시장 |
| 거래조건 | 표준화된 시장 | 당사자 간 합의 |
| 증거금제도 | 증거금 필요 | 없음 |
| 가격형성 | 매일 형성됨 | 계약체결시 한 번 형성 |
| 이행보증 | 거래소가 이행보증 | 거래당사자 신용 |
| 결제방식 | 일일정산 | 만기일정산 |
| 규제방식 | 엄격한 규제 | 자율규제 |
| 상품인수도 | 반대매매 청산 현금인도 |
만기일에 실물 인수도 |
(4) 일일정산제도
매일매일 정산되는 가격을 기준으로 선물거래자와의 미청산계약(미결제약정)에 대한 손익을 계산하여 증거금에 반영
(5) 증거금제도
개시증거금(총계약금액의 5%-15% 수준), 유지증거금(개시증거금 75%-80% 수준), 추가증거금(마진콜, 개시증거금 수준까지 납부해야 함), 초과증거금(인출가능)
(6) 미결제약정수량(open interest)
특정한 선물계약에 대한 청산되지 않은 계약의 수
(7) 선물매입표지션과 매도포지션
손익의 크기가 같고 부호가 반대인 제로섬 게임
2. 선물 균형방정식
(1) 현-선물 등가식(Spot-Futures parity)
$ F = S_0(1+r_f) $
선물매입 = 현물매입 + 차입(무위험채권 매도)
선물매도 = 현물매도 + 대출(무위험채권 매입)
🖍 무차익원리(no arbitrage)에 의해 유도됨
🖍 좌변과 우변의 차이의 절대값은 만기시점의 차익거래이익
(2) 보유비용 모형
현-선물 등가식에 보유비용을 고려한 모형(현물에 대한 보관비용이 존재할수록 선물이 유리)
1) 수익률 형태로 주어진 경우
$ F = S_0(1+r_f+u-y) $
🖍 u는 보관비용(수익률 형태), y는 보유편익(수익률 형태)
2) 현금흐름 형태로 주어진 경우
$ F = S_0(1+r_f)+U_T-Y_T $
🖍 $U_T$는 보관비용의 만기가치, $Y_T$는 보유편익의 만기가치
(3) 거래비용모형(범위)
$ S_a(1+(1-\alpha)r_l-TC \leq F \leq S_b(1+r_b)+TC $
거래비용이 존재하면 균형가격이 단일 값이 아닌 범위로 결정됨
📝 주가선물지수
$ F = S(1+r_f-d) \frac{T}{365} $
📝 금리선물
$ F = S(1+r_f) - I_T - D_T $
3. 선물가격$F$과 기대현물가격$E(S_T)$

(1) 기대가설(expectation)
$ F = E(S_T) $
🖍 위험중립자($ k=r_f, \beta=0 $)
(2) 정상적 백워데이션 가설(normal backwardation)
$ F < E(S_T) $
🖍 위험기피자($ k>r_f, \beta>0 $)
(3) 콘탱고 가설(contango)
$ F > E(S_T) $
🖍 위험기피자($ k<r_f, \beta<0 $)
🖍 위험프리미엄은 여전히 양수이지만 베타가 0보다 작기 때문에 발생하는 현상임
(4) 순헤지가설(net hedging)
어느 쪽 비중이 더 큰가에 따라 달라짐
4. 선물거래전략(헤지, 투기거래, 차익거래)
(1) 헤지
현물거래와 수량이나 금액의 반대포지션을 취하는 것
🖍 매입헤지(현물시장 매도포지션+선물계약 매입포지션), 매도헤지(현물시장 매입포지션+선물계약 매도포지션)
📝 완전헤지와 불완전헤지
완전헤지(가격위험이 완전히 헤지되는 경우), 불완전헤지(가격위험이 여전히 존재하는 경우)
🖍 완전헤지는 현물과 선물의 상관계수가 +1인 경우에만 가능
📝 직접헤지와 교차헤지
직접헤지(현물자산과 선물계약의 대상물이 동일한 경우), 교차헤지(현물자산과 비슷한 가격변동 패턴을 보이는 일종의 매개자산을 통한 헤지)
(2) 선물의 헤지수량 결정
현물 포지션에 대해 반대 포지션을 취해서 헤지 수량을 결정
1) 가격변동액 척도
$ \Delta V = \Delta S + h \Delta F $
📝 헤지비율(HR)

📝 헤지수량(N)
헤지비율 x (헤지대상 현물자산 규모 / 선물 1계약 거래단위)
2) 가격변동률 척도

📝 헤지비율(HR)

📝 헤지수량(N)
헤지비율 x (헤지대상 현물자산 규모 / 선물 1계약 거래단위)
(3) 투기거래
단순투자(레버리지 기능), 베이시스 거래(현물가격과 선물가격의 가격차이를 이용), 스프레드 거래(근원물과 원월물의 시간가치 차이를 이용)
(4) 차익거래
현-선물 등가식이 성립하지 않을 때 차익거래하는 방식
🖍 $F < S_0(1+r_f) \quad 또는 \quad F > S_0(1+r_f)$
🖍 차익거래 이익(만기시점 기준) = $|F-S_0(1+r_f)|$
5. 주가지수선물
(1) 균형방정식
보유비용모형으로부터 유도됨(배당금이 주식현물에 대한 보유편익이기 때문)


🖍 등호가 성립하지 않으면 차익거래 발생
(2) 헤지거래
1) 단순헤지

2) 베타헤지


3) 최소분산헤지


4) 목표 베타 관리

🖍 목표 베타 관리는 우변에 (-)가 붙지 않음에 주의
6. 금리선물
(1) 단기금리선물
| $ \sideset{_0^}{}S_2 $ | ||
| $ S_0 $ | $ \sideset{_0^}{}S_1 $ | $ \sideset{_1^}{}f_2 $ |
$ F = S_0(1 + \sideset{_0^}{}S_1) = \frac{100}{1 + \sideset{_1^}{}f_2} $
$ \sideset{_1^}{}f_2 = BEY(Bond Equivalent yield) $
(2) 장기금리선물
$ F = S(1+r_f) - I_T = (S - I)(1+r_f) $
(3) 헤지
1) 듀레이션 헤지

2) BPV 헤지
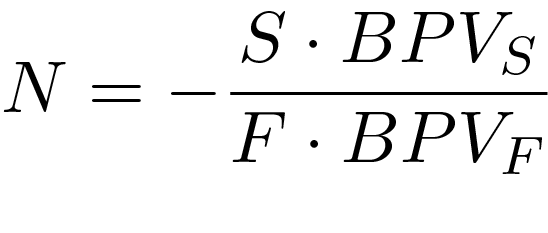
(4) 목표 듀레이션 관리

🖍 목표 듀레이션 관리는 우변에 (-)가 붙지 않음에 주의
7. 스왑의 의의와 종류
(1) 스왑의 의의
두 당사자가 미래의 현금흐름을 맞교환하는 것
(2) 스왑의 종류
금리스왑과 통화스왑으로 구분됨
📝 금리스왑
금리스왑은 변동금리와 고정금리를 교환(이자만 교환)
📝 통화스왑
통화스왑은 변동이든 고정이든 상관없이 교환(금리와 이자를 모두 교환)
(3) 스왑의 효익
변동금리인 당사자와 고정금리인 당사자의 이자율위험 헤지, 상대적 비교열위가 있는 금리로 자금조달시 차입비용 절감효과(데이비드 리카도의 비교우위원리)
(4) 스왑 가치
1) 스왑가치(자기자본가치)
$ V_{swap} = | V_{fix} - V_{float} | $
2) 스왑듀레이션(자기자본듀레이션)
$ D_{swap} = wD_{fix} + (1-w)D_{float} $
3) 금리선도계약의 관점에 의한 스왑 가치평가
$ V_{swap} = \sum \frac{CF_t^{fix} - CF_t^{float}}{(1 + \sideset{_0^}{}S_t)} $
4) 채권포트폴리오 관점에 의한 스왑 가치평가
$ V_{swap} = V_{외화} \times S_0 - V_{원화} $
5) 금리선도계약의 관점에 의한 스왑 가치평가
$ V_{swap} = \sum \frac{|CF_t^* \times S_t - CF_t|}{(1 + \sideset{_0^}{}S_t)^t} $
'재무관리 이론' 카테고리의 다른 글
| [합병과 취득] M&A 기초, 합병의 평가, 주식교환비율 결정, M&A와 이익성장률 (0) | 2021.12.21 |
|---|---|
| [국제재무관리] 국제재무관리 기초, 환율결정이론, 통화선물 (0) | 2021.12.20 |
| [채권가치평가와 투자전략] 채권 기초, 채권수익률, 이자율 위험구조, 이자율 기간구조, 듀레이션과 볼록성, 채권투자전략 (0) | 2021.12.20 |
| [불확실성하의 자본예산과 배당정책] 위험조정할인율법, 확실성등가법, MM모형과 하마다모형, 효율적 자본시장 가설, 배당정책 (0) | 2021.12.20 |
| [MM모형과 자본구조이론] 레버리지도, 하마다모형, 원천별 자본비용, MM모형과 전통적 자본구조이론, 현대 자본구조이론 (0) | 2021.12.20 |
블로그의 정보
펭귄협동조합
펭협